最高のコレクション 底辺×高さ÷2 台形 237424

台形の計算式ですが (上底＋下底）×高さ÷2＝面積 となるところが （上底＋下底）×高さ＝面積 となって表示されます。 算出されている面積は問題ないのですが 表記される計算式に「÷2」が表示されないように 思われます。 ご確認いただければと思います。底辺×高さ＝面積 a×h=a h ひし形の面積 対角線×対角線÷2＝面積 a×b 2 1 a b 円の面積 半径×半径×314＝面積 r ×r ×S＝Sr 2 円の周りの長さ（円周） ①直径×314＝円周 r ×2×S＝2Sr 扇形の弧の長さと面積 360 x ＝弧の長さ ℓ=2Sr × 360 x台形の面積＝（上底下底）×高さ÷2 のためです。実際に、下図の台形の底辺（下底）を計算します。 面積が30、高さが5、上底が2です。前述した公式に当てはめると 30＝（2下底）×5÷2 下底＝12－2＝10 です。

台形の面積の公式 小学生に教えるための分かりやすい解説 数学fun

底辺×高さ÷2 台形

底辺×高さ÷2 台形-平行四辺形の面積＝底辺×高さ ひし形の面積＝対角線×対角線÷2 台形の面積＝(上底＋下底)×高さ÷2 ※台形の面積は特に忘れやすいので注意が必要です。 正方形はひし形でもあるので 正方形の面積＝対角線×対角線÷2 でも求められることも覚えておくといい用語で表現するなら（上底 下底）×（高さ）÷ 2 である。 この公式は、台形を対角線で2つに分けたときの各々の三角形の面積が ah /2 および bh /2 であることから得られる。 この公式を導く別の方法としては、まず2つの台形を上底と下底以外の辺（上図での AD もしくは BC）同士を重ね合わせて平行四辺形をつくる。 そしてその平行四辺形の面積（＝（底辺）×（高さ））は ( a b) h であり、

算数の思考 台形の面積 敵は我に在り

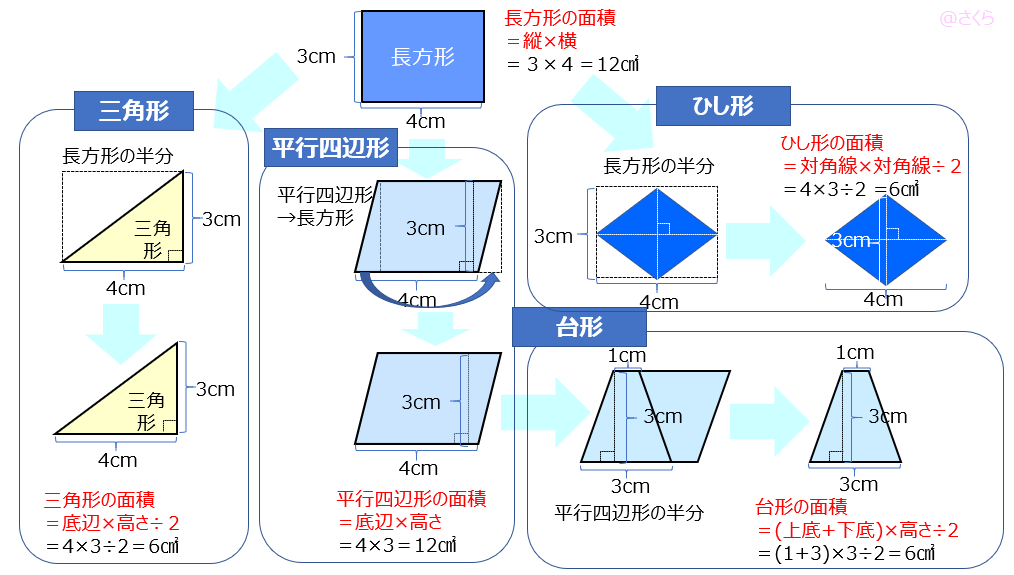
三角形の面積＝底辺×高さ÷2 上の図のように、高さを表す長さが図形の外側に表示されることもあります。 お子さんがよくまちがえるところですので 底辺と高さが必ず垂直の関係になっていることを強調して教えましょう。4つの面積の公式をおさらいしておきましょう。★三角形底辺×高さ÷2 ★平行四辺形平行四辺形だけは÷2しない！底辺×高さ ★台形（上底＋下底）×高さ÷2 ★ひ解説 三角形、平行四辺形、 ひし形、台形の面積 年 組 名前 平行四辺形の面積＝底辺×高さ 三角形の面積＝底辺×高さ÷2 台形の面積＝（上底＋下底）×高さ÷2 ひし形の面積＝一方の対角線×もう一方の対角線÷2 取り組んだ日 月 日 この場合、ななめの辺 の長さは使いません。 底辺 高さ プリントを回転させよう。 が下です。 高さ 底辺 三角形は2つ合わせると 平行四辺形になります。 平行四辺形の半分

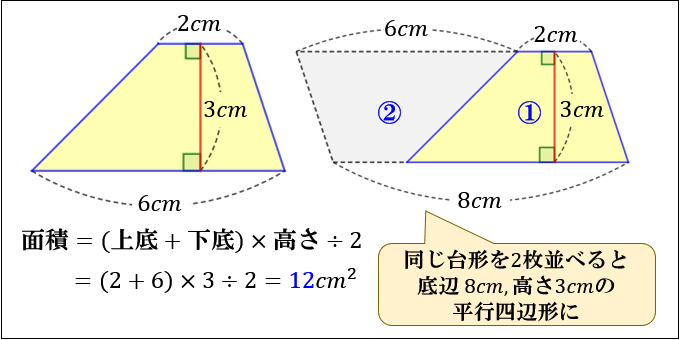
つまり (A＋6)×4÷2という式になります。 台形の左上の点を結ぶと 三角形 ができることに気づかせます。 この三角形の面積は、底辺が（A＋6)で高さが4cmです。 三角形の面積は底辺×高さ÷2なので (A＋6)×4÷2という式になります。 以上のような説明がお子 平行四辺形の面積は、 「面積 底辺 高さ」 「 面 積 = 底 辺 × 高 さ 」 で求められます。 たとえば、「底辺 4 c m ,高さ 3 c m の平行四辺形」の面積は 4 × 3 = 12 c m 2 となります。 これは、平行四辺形の右端の直角三角形を切り取って左側に移すと 「たて 3 c m平行四辺形の面積 ＝ 底辺 × 高さ 三角形の面積 ＝ 底辺 × 高さ ÷ 2 台形の面積 ＝（上底＋下底）× 高さ ÷ 2 台形の面積 点D を点A に近づけて重ねると 三角形の面積 台形の上底を cm とみることで，台形の公式を使って三角形の面積を

 16×11÷2＝（㎠） 答え ㎠ 問題⑤ 面積が63㎠である、次の三角形の高さを求めましょう。 《三角形の高さの求め方》 この三角形の底辺の長さは9cm、高さは cm、面積は63㎠なので、これらを三角形の面積を求める公式に当てはめます。 すると よっての長さはそれぞれいくつになるでしょう？ この問題は、テストの最終問題ですので、なかなか難しいですね。 三角形の面積：底辺×高さ÷2 台形の面積：（上底＋下底）×高さ÷2 1辺の長さの比は、底辺や高さの比と同じなのでxとして赤の？ 底辺×高さ÷2 で求めることができます。 三角形は平行四辺形を対角線で切って半分にした形 です。同じ形の三角形を逆さまにして2つを合わせてみるとすぐ分かります。 ですから、まず平行四辺形の面積（底辺×高さ）を計算して、その半分にするのです。

なぜ 三角形の面積は 底辺 高さ 2 なのか を説明します おかわりドリル

3

高さp 高さ 高さ 底辺 上底 対角線 ひし形の面積＝対角線×対角線÷2（教5下p13） 三角形の面積＝底辺×高さ÷2（教5下p6） 平行四辺形の面積＝底辺×高さ（教5下p10） 台形の面積＝（上底＋下底）×高さ÷2（教5下p12） （解答例1） 4＋12＝16台形の面積＝上底を底辺とする三角形＋下底を底辺とする三角形 ＝ 上底 ×高さ÷2＋ 下底 ×高さ÷2 ＝（ 上底 ＋ 下底 ）×高さ÷2。 台形の面積の公式は、上底を底辺とする三角形と下底を底辺とする三角形の面積の和と考えても成り立つということですね。 三角形だと底辺×高さ÷2なのに、台形だと上底＋下底ってなるのか。 何年の学習指導要領で小中学校を過ごしてきたのだろう。 一時期台形の面積がなかった時期があったと記憶している。 台形を対角線で切り離す。面積は2つの 三角形の和だ。 (上底下底)×高さ÷2 = 上底×高さ÷2＋下底×

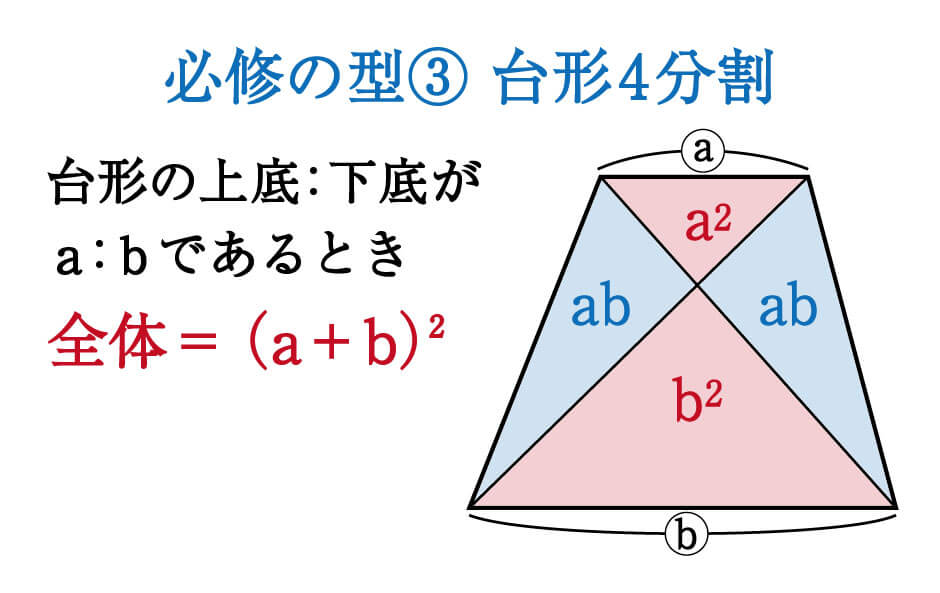
数学 台形を4分割した図形パターン 面積比 集中特訓 3 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo

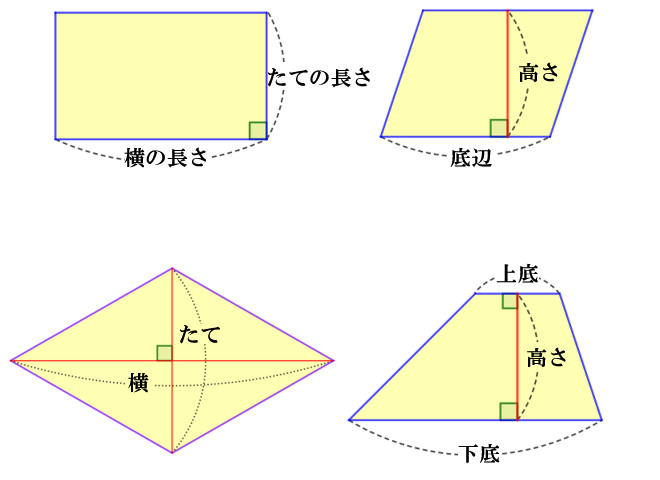
四角形の面積の求め方 公式とその仕組み 小学算数 アタリマエ

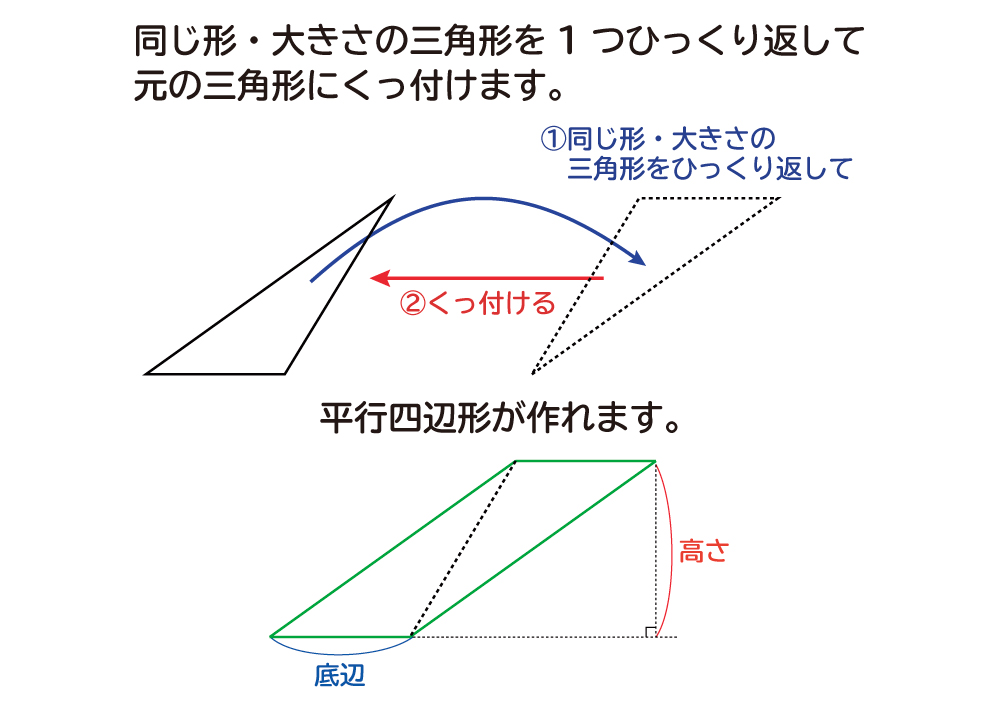
平行四辺形の面積は，「底辺×高さ」で求められ ます。 右の図において，底辺は30cmで，高さはcm 2）になり ます。 基本4 (2) (2)では，底辺を25cmにします。 そのときの高さはχcmになります。 面積は，(1)で求めた通り，600cm2です。 平行四辺形 ＝ 底辺 × 高さ 三角形 ＝ 底辺 × 高さ ÷ 2 台形 ＝ （上底 下底）× 高さ ÷ 2 ひし形 ＝ 対角線 × 対角線 ÷ 2 円 ＝ 半径 × 半径 × 円周率 弧 ＝ 半径 × 半径 × 円周率 × 弧の角度 ÷ 360 2 体積 立方体 ＝ 一辺 × 一辺 × 一辺 直方体 ＝ 縦 × 横 なぜ、どんな形をした三角形でも、その面積は 「三角形の面積 底辺 高さ 」 「 三 角 形 の 面 積 = 底 辺 × 高 さ ÷ 2 」 で求まるのでしょうか。 形がちがう2種類の「底辺 5 c m 高さ 2 c m の三角形」を通じてみていきましょう。 ※1マス 1 c m 初めに、同じ形をした三角形をもう1つ用意します。 それをひっくり返して 重ねると 底辺 5 c m 、高さ 2 c m の平行四辺形になることが分かりま

図形の問題は公式の暗記に頼らないようにする まなびのへや

平行四辺形の面積の求め方 公式と計算例

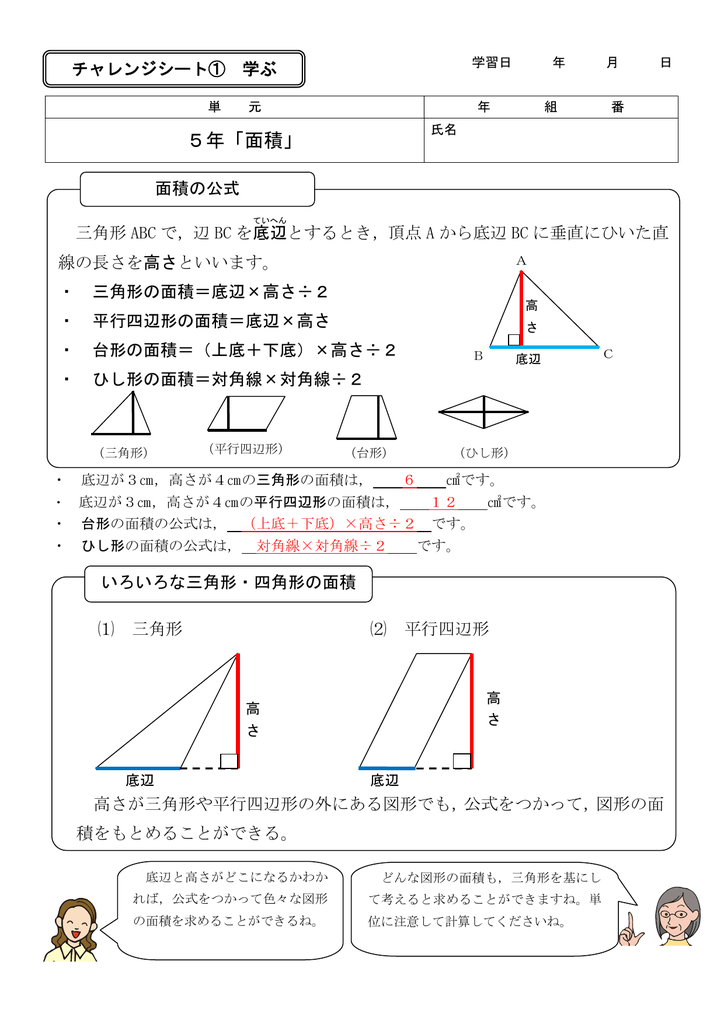
・ 三角形の面積＝底辺×高さ÷2 ・ 平行四辺形の面積＝底辺×高さ ・ 台形の面積＝（上底＋下底）×高さ÷2 ・ ひし形の面積＝対角線×対角線÷2 面積の公式 ⑴ 三角形 ⑵ 平行四辺形 高さが三角形や平行四辺形の外にある図形でも，公式をつかって，図形の面 積をもとめることができる。 いろいろな三角形・四角形の面積 チャレンジシート① 学ぶ 底辺と高さがどこになるかわか れば，公式をつかって平行四辺形の底辺は（上底下底）で高さは元の台形の（高さ\(÷2\)）です。 なので台形と面積が等しいこの平行四辺形の面積は、 『（上底下底）×高さ\(÷2\)』 となります。 丸暗記していたらいざ本番で忘れた時に解けなくなるので、毎回頭の中で図形の変形をイメージしながら解くのをオ台形の面積 S の公式でよく知られているものは = () である。ここに a, b, h は上底、下底、高さに対応する長さである。用語で表現するなら（上底 下底）×（高さ）÷ 2 である。この公式は、台形を対角線で2つに分けたときの各々の三角形の面積が ah/2

台形とは 定義や 台形の面積の公式をわかりやすく解説 受験辞典

台形の面積の公式 小学生に教えるための分かりやすい解説 数学fun

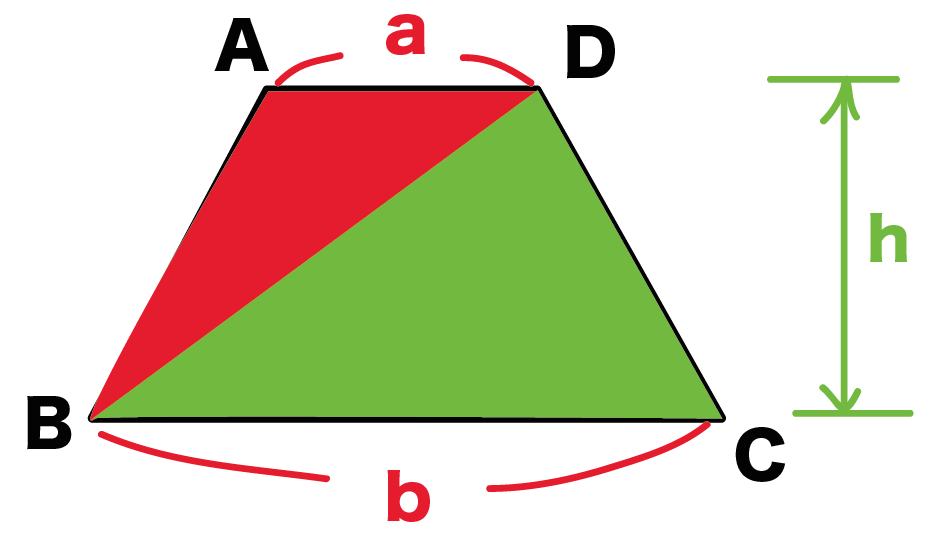
台形の面積 三角形の面積の求め方を使って、下の図の赤い部分の台形の面積を求められます。 台形も、平行四辺形と同じように、対角線を1本引き、2つの三角形に分けます。 片方の三角形に注目してみましょう。 次の図でオレンジ色の三角形の面積を考え＝底辺×高さ 台形の面積 ＝（上底＋下底）×高さ÷2 で求めることができます。 8cm 4cm 4cm 6cm 3cm ア イ ㋐ ㋑ 3 5cm 8cm 6cm ←正方形の対角線は垂 すい 直に交わ るので，ひし形の面積と同じよ うに， 対角線×対角線÷2 で求めることができます。 4 ←三角形の面積 2 だから、α＝2／π ＝底辺×r s：もしかしたら、この船のような形の面積がわかれば表面積を求めることができるのじゃない？ ⇒105、球の表面積と舟形多円錐図法 目次へもどる＝（下底＋上底）×高さ÷2＝（上底＋下底）×高さ÷2 台形の面積が導き出される

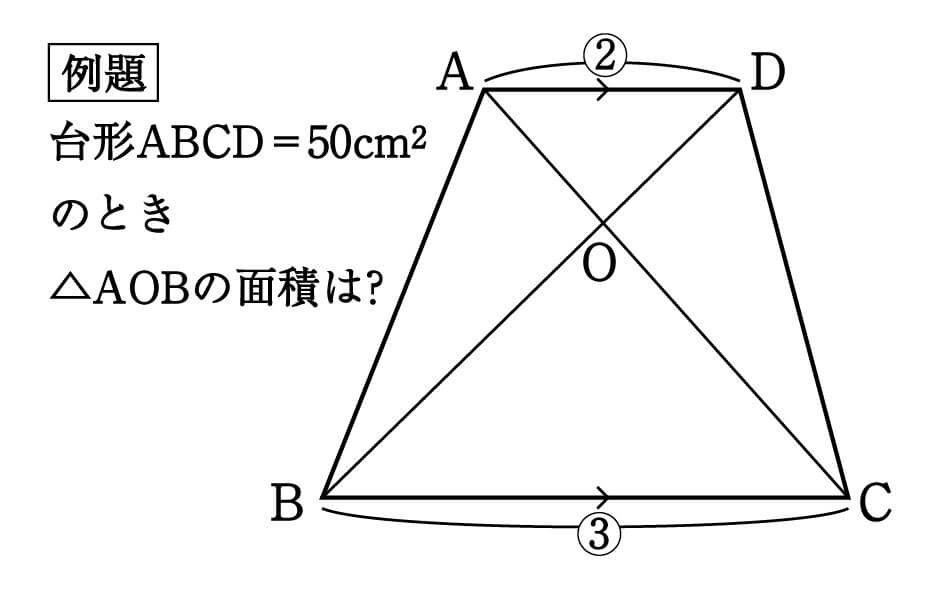
数学 台形を4分割した図形パターン 面積比 集中特訓 3 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo

三角形と台形の面積

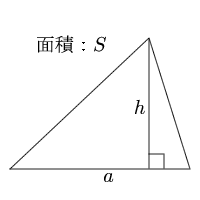
 {（下の辺）×（下の辺） （下の辺）×（上の辺） (上の辺) × (上の辺) }×高さ÷3 ってことさ。 たとえば、下の辺が4cm、上の辺が2 cm、高さ6cmの正四角錐台ABCDEFGHがあったとしよう。 この立体の体積は、 1/3 h ( a^2 ab b^2 ) = 1/3 × 6 × ( 4^2 4 × 2 2^2) = 2 × ( 16三角形の底辺が3、高さ4、三角錐の高さが5のとき 三角錐の体積＝3×4÷2×5÷3＝10cm 3 です。 まとめ 今回は体積の公式について説明しました。体積の公式は色々あると思いがちですが、基本の公式は「底面積×高さ」「底面積×高さ÷3」です。右 図1 のような三角形の面積は、いずれも （底辺）×（高さ）÷2 で求められます。 次のように分数の形で書くこともできます。 （面積）＝ （底辺）×（高さ）2nnnnnnnnnnnnnnn (1) 2で割ることを忘れる答案が多いので注意しましょう。 右 図2 の三角形の

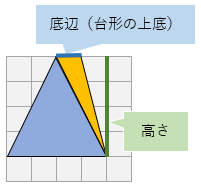
台形の面積の求め方 算数の公式は覚えるな Sundry Street

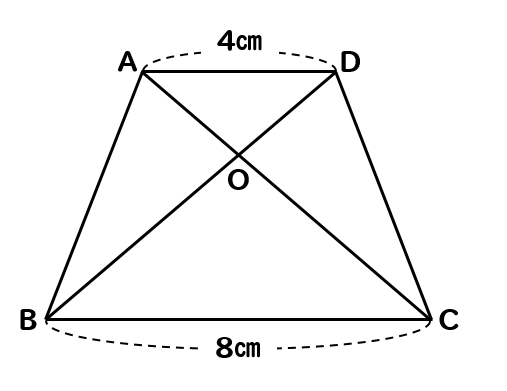
相似 台形と面積比の問題を徹底解説 数スタ

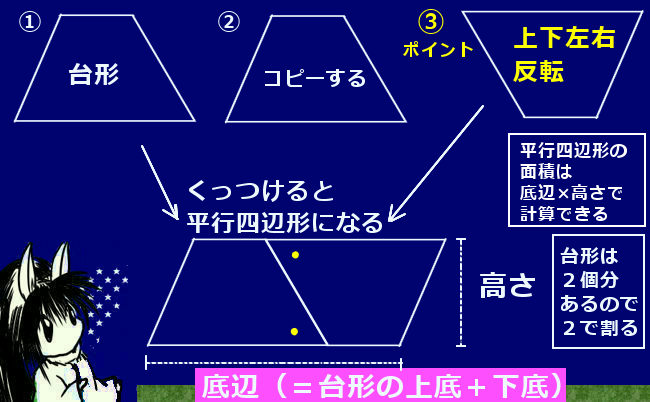
 底辺×高さ÷2ってのは 三角形の面積の式ですから直角三角形にこだわる必要はありませんよ 対角線を一本引いてみてください すると底辺をa、高さhの三角形と、底辺をb、高さhの三角形の二つに切ることができるでしょ 底辺aの三角形の面積はah/2 底辺bの三角形の面積はbh/2 二つの和が台形の面積を求める公式 面積= (上底下底)×高さ÷2 この公式の理屈としては、まず台形の上底から下に線を引き1つの四角形と2つの三角形に分離します。 片方の三角形を左右上下反転して逆の三角形にくっつけると大きな四角形ができあがります。 この 平行四辺形の面積＝底辺×高さ 三角形の面積 ＝底辺×高さ÷2 台形の面積 ＝（上底下底）×高さ÷2 ひし形の面積 ＝対角線×対角線÷2 直角に注目して 「底辺」「高さ」 「対角線」を きちんと見つける かずのかず 以上、「算数嫌いな人が、 算数を楽しく好きになって欲しい」 かずのかずでした 小5算数「割合」の問題 どこよりも簡単な解き方・求め方 小5算数「単位量あたり

高さがわからない台形の面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

台形とは 定義や 台形の面積の公式をわかりやすく解説 受験辞典

形の面積＝底辺×高さで底辺のところが台形の上底＋下底になってい ますだから台形の面積＝（上底＋下底）×高さ÷2です 子供たちは上のように今まで学習した ことを基に t習っていない台高さが三角形の外にあるときでも面積公式が適用できること 4 8 台形の面積の求め方 9 台形の面積公式と適用 10 ひし形の面積の求め方及びひし形の面積公式と適用 5 11 三角形の底辺の長さを一定にして，高さを変えたときの面積と高さの関係の理解 12 四角柱 ⇒ (上底下底)÷2×高さ 三角柱 ⇒ 底辺×高さ÷2 円錐 ⇒ 半径×半径×314 四角錐 ⇒ (上底下底)÷2×高さ 三角錐 ⇒ 底辺×高さ÷2 各図形の底面積の具体的な計算方法を勉強しましょう。※下記も参考になります。 底面積の求め方は？高さ 底辺 上底 高さ 台形

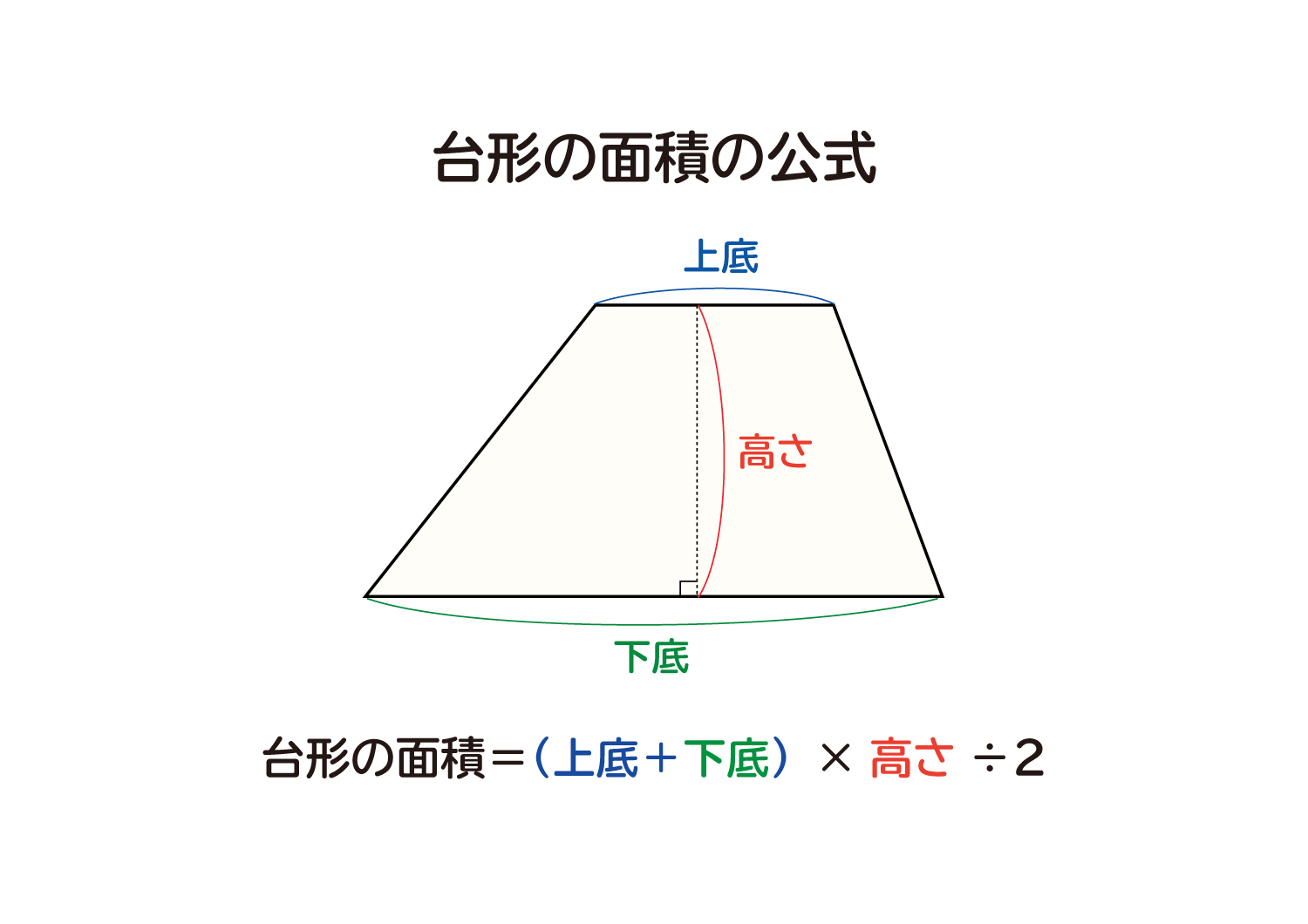
なぜ 台形の面積は 上底 下底 高さ 2 なのか を説明します おかわりドリル

四角形の面積の求め方 公式とその仕組み 小学算数 アタリマエ

 三角形は「底辺×高さ÷2」 平行四辺形は「底辺×高さ」 台形は「(上底下底)×高さ÷2」 ひし形は「縦の対角線×横の対角線÷2」 という公式を覚えておきましょう。また、図形の「どこが高さになるのか」を理解しておく必要があります。斜めの線ではなく 長方形 = たて × 横 三角形 = 底辺 × 高さ ÷ 2 平行四辺形 = 底辺 × 高さ 台形 = ( 上底 下底 ) × 高さ ÷ 2 ひし形 ＝ 対角線 × 対角線 ÷ 2 円 = 半径 × 半径 × 円周 体積 角柱 ・ 円柱 = 底面積 × 高さ 角錐 ・ 円錐 = 底面積 × 高さ ÷ 2 単位あたりの 量 速さ面積事項 （長方形の面積）＝（縦）×（横） （正方形の面積）＝（一辺）×（一辺） （三角形の面積）＝（底辺）×（高さ

2

算数の思考 台形の面積 敵は我に在り

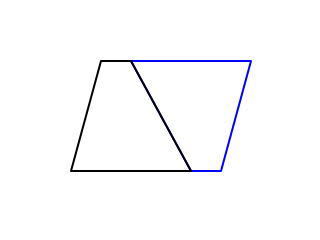
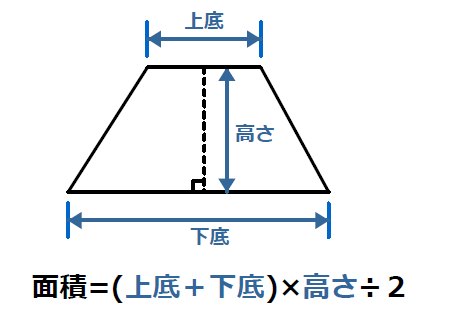
三角形 ＝底辺×高さ÷2 正方形 ＝1辺×1辺または，対角線×対角線÷2 長方形 ＝たて×横 平行四辺形＝底辺×高さ 台形 ＝（上底＋下底）×高さ÷2 ひし形 ＝対角線×対角線÷2 〃 外角の和＝360度 目 次 反復基本1 (1)①p1 反復練習1 p10三角形の面積＝底辺×高さ÷2 平行四辺形の面積＝底辺×高さ ひし形の面積＝対角線×対角線÷2 台形の面積＝（上底＋下底）×高さ÷2 円の円周の長さ＝直径×円周率 円の面積＝半径×半径×円周率 おうぎ形の弧の長さと面積は、円の円周の長さや面積の  公開 ・台形の面積計算 上底と下底と高さから台形の面積を計算するプログラムを解説します。 台形の面積は、（上底＋下底）×高さ÷2で計算できます。 下図のように、台形の右側に、上と下を逆にした台形をくっつけて平行四辺形を作ります。

盲点の英単語 その8 1 三角形 台形の面積を求める 中学の英語をあなどってはいけない

台形の面積の公式 小学生に教えるための分かりやすい解説 数学fun

台形の面積を求める公式は、s = {(上底)(下底)}×(高さ)÷2 で表されます。このページでは、台形の面積の求め方を、計算問題と共に説明しています。また、公式の導き方も説明しています。台形の面積の公式は，「（上底＋下底）×高さ÷2」です。 右図で，上底は5cm，下底は cm，高さは8cmです。 台形の面積は56cm2であることが問題に書いてありましたから， あとは逆算をするだけです。 14－5＝9（cm） 基本1 (3)

５年算数三角形と四角形の面積2 教え方 台形 ひし形

高さがわからない台形の面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

台形の高さの求め方

2

数学 台形を4分割した図形パターン 面積比 集中特訓 3 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo

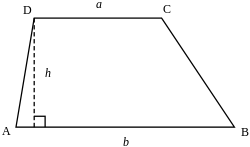
台形 Wikipedia

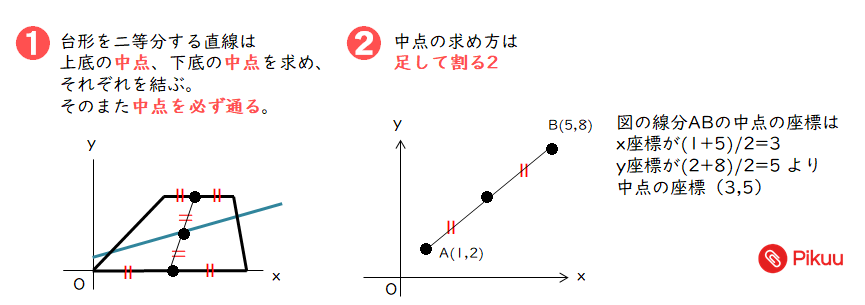
中学数学 二次関数の台形の二等分線を求める練習問題 Pikuu

台形の公式は必要か

台形の面積の求め方 公式と計算例

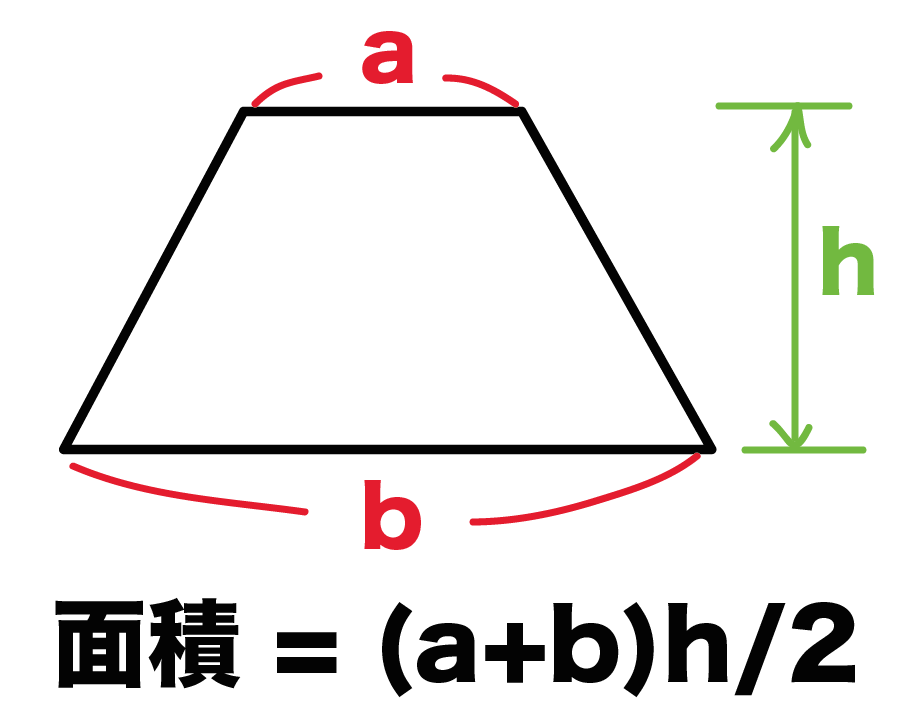
高さがわからない台形の面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

台形の面積の求め方 公式と計算例

５年算数三角形と四角形の面積2 教え方 台形 ひし形

三角形の面積比を解説 平面図形が苦手な人でもわかりやすい解き方 基本編 中学受験ナビ

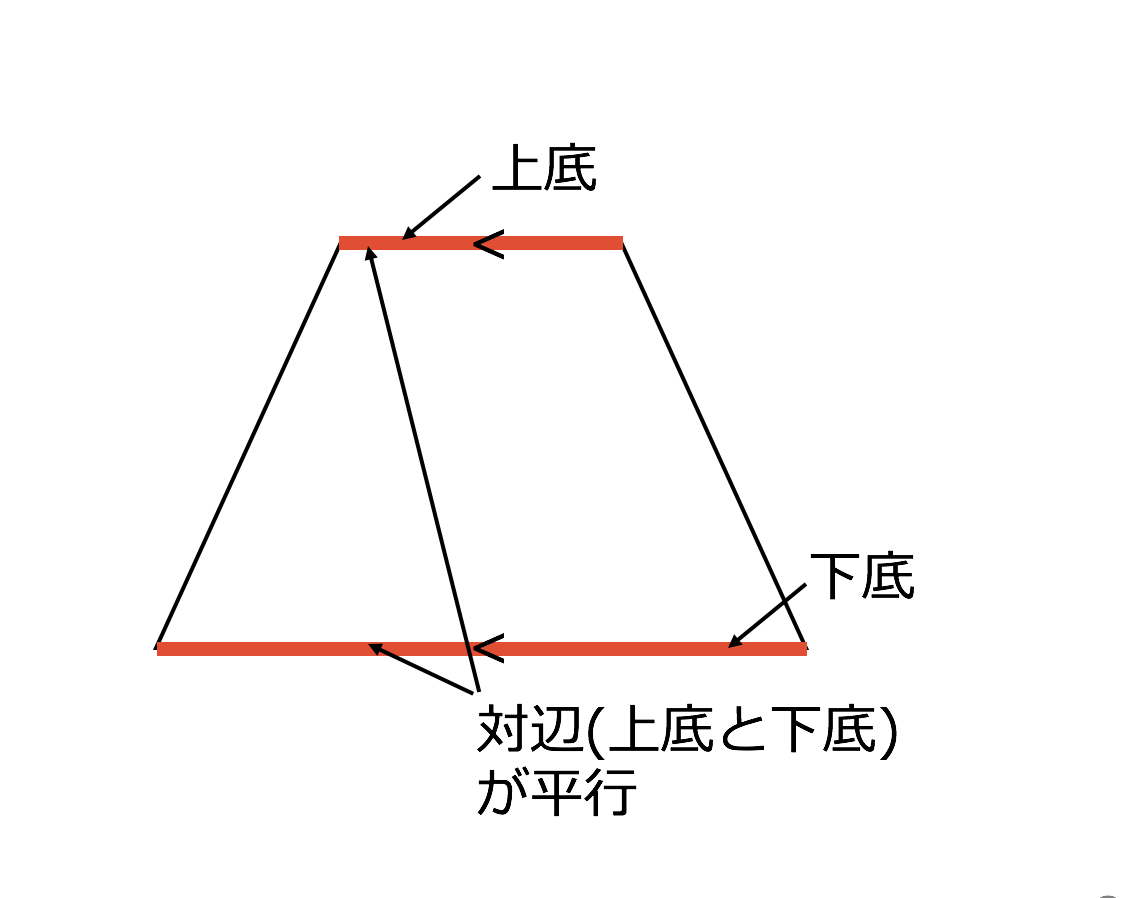
3分で分かる 台形の面積の求め方 公式についてわかりやすく 合格サプリ

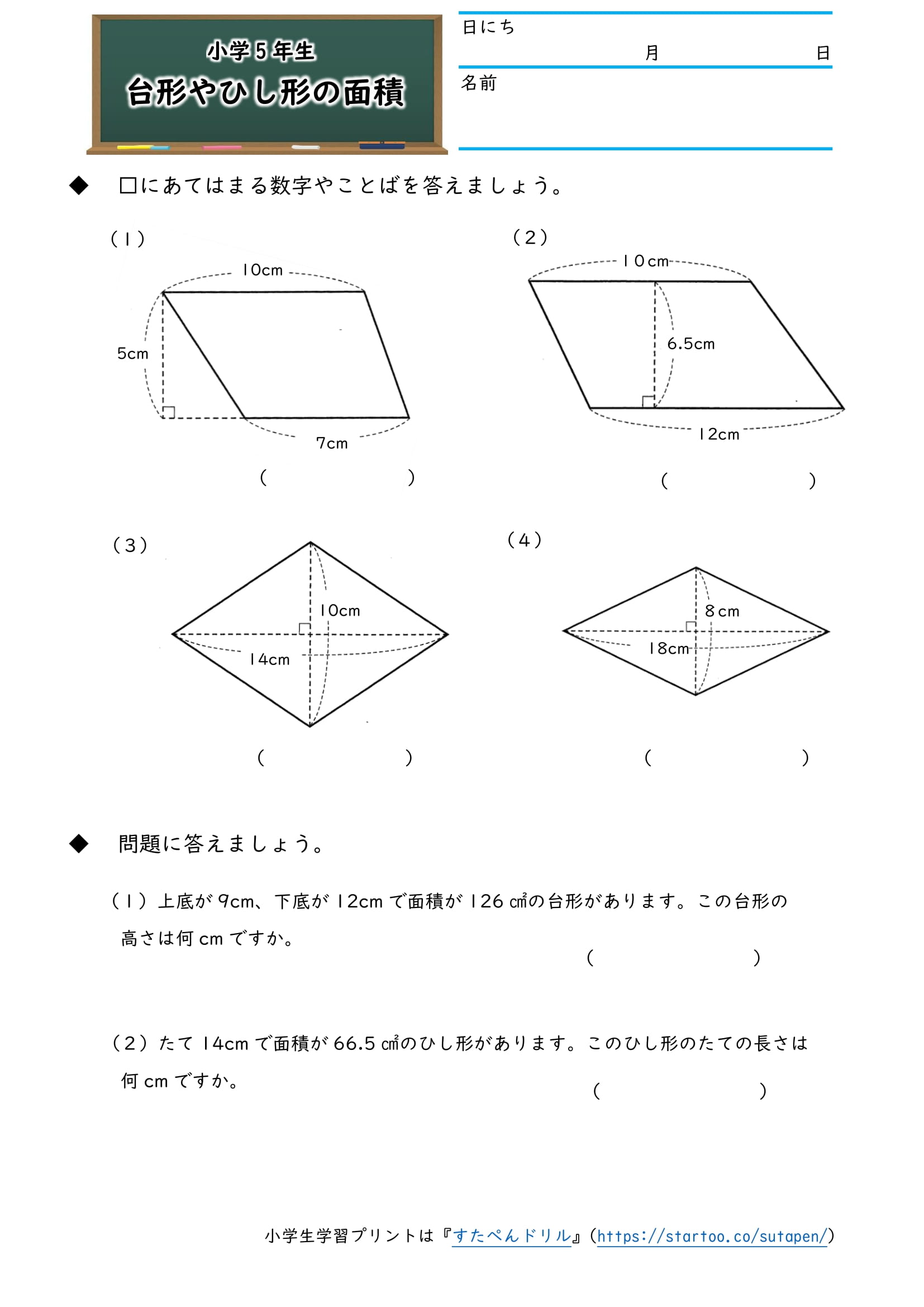
小5算数 四角形と三角形の面積 の学習プリント 練習問題 無料ダウンロード 印刷

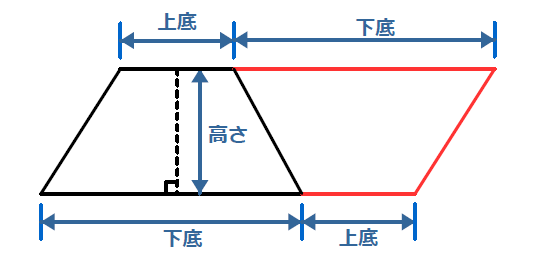
台形の面積計算 ゆるゆるプログラミング

台形の任意の高さにおける上辺の長さ 相似関係の2つの台形の高さがそれぞれ Okwave

2

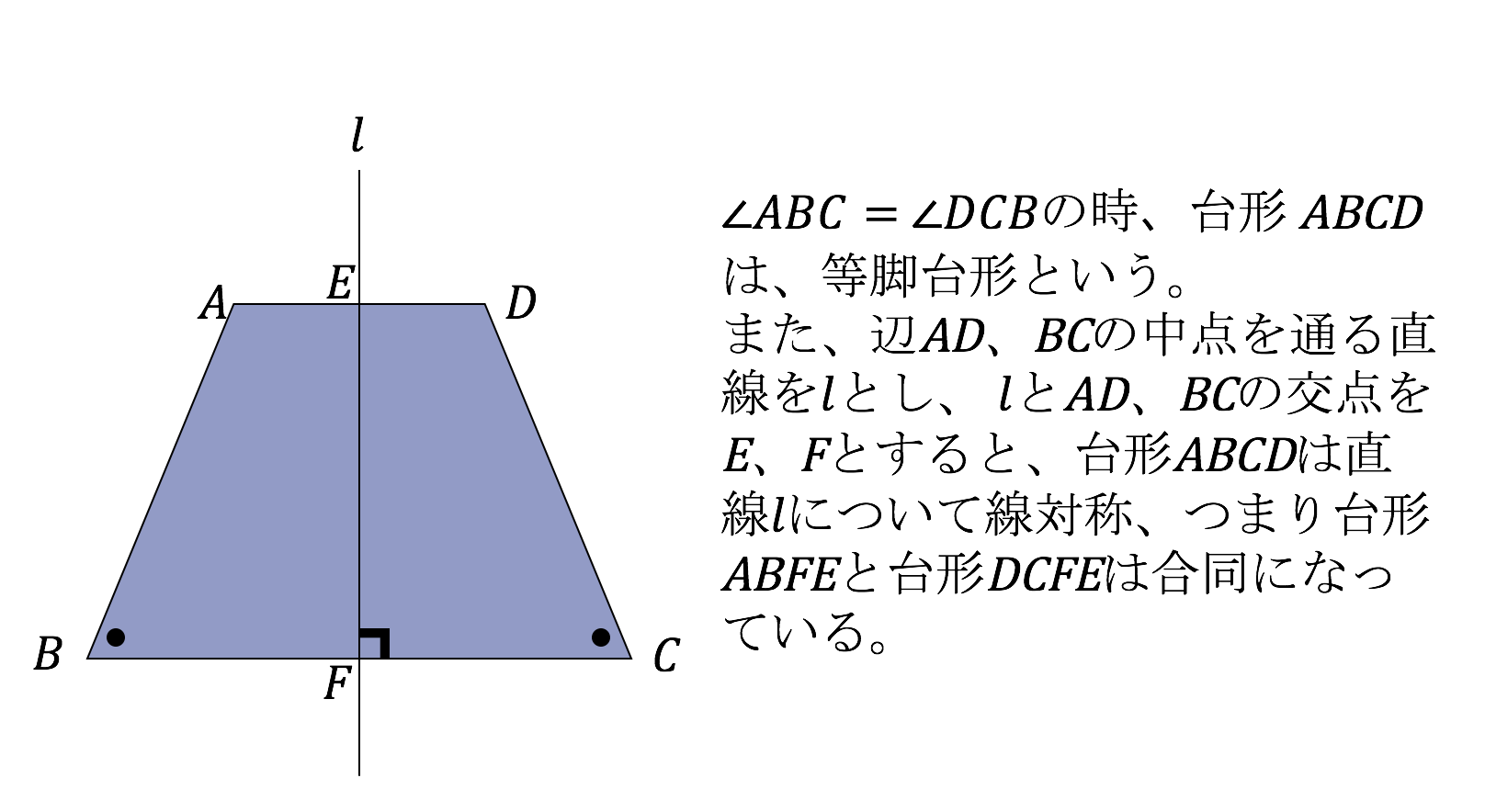
3分で分かる 台形の面積の求め方 公式についてわかりやすく 合格サプリ

簡単公式 台形の面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

面積 の記事一覧 みけねこ小学校

高さがわからない台形の面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

四角形の種類と性質 面積の公式について 中学受験 ゲーム大好き息子の偏差値32からの挑戦

三角形の底辺と高さ 面積の計算 計算サイト

台形の面積計算 ゆるゆるプログラミング

台形の面積公式 算数と図形 理数系学習サイト Kori

2

5年 面積

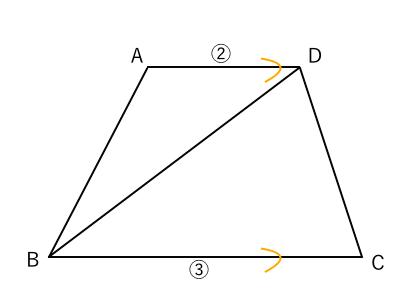
小学6年生 算数の問題です 台形abcdの面積の求めかたを詳しく教えて下さい Yahoo 知恵袋

高さがわからない台形の面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

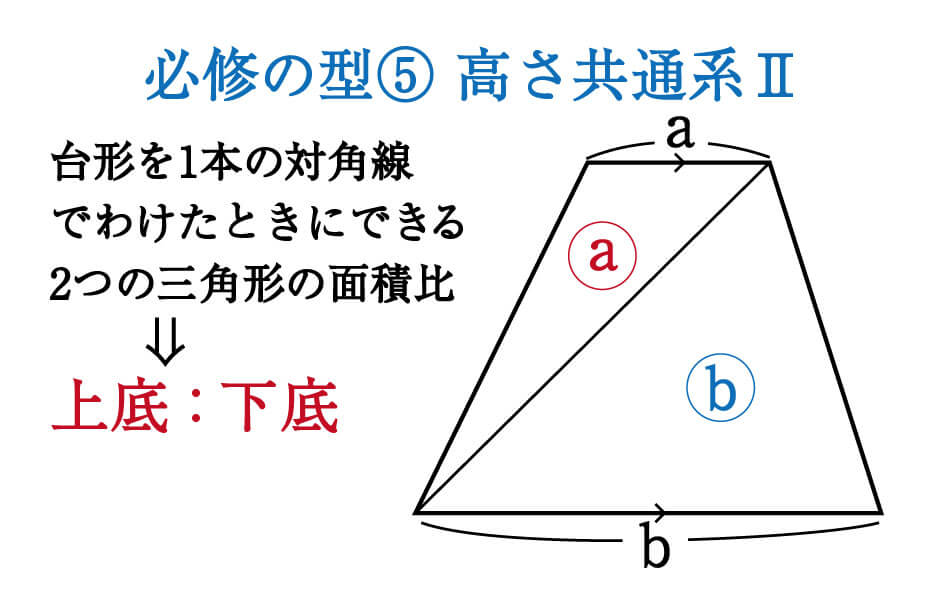
数学 対角線の入った台形 一角共有の三角形 面積比 集中特訓 6 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo

2

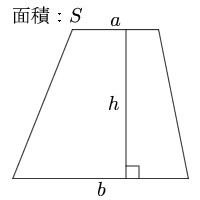
台形 面積の計算 計算サイト

台形の底辺は 1分でわかる意味 計算 求め方 上辺 面積との関係

台形とは 定義や 台形の面積の公式をわかりやすく解説 受験辞典

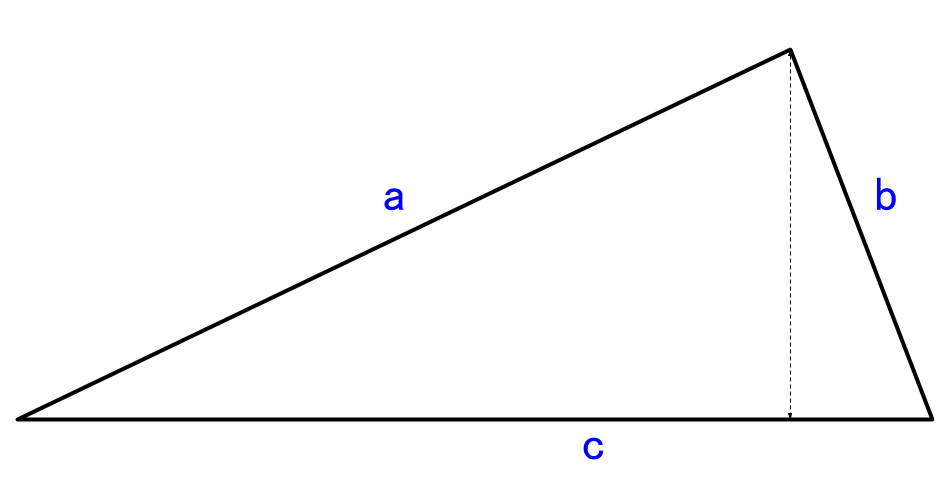
ヘロンの公式 計算機 三角形の面積と高さを 3辺の長さから計算します やまでら くみこ のレシピ

今すぐ教えてください 少しでいいですm M Clearnote

高さがわからない台形の面積の求め方を教えてください 高さがわか Yahoo 知恵袋

台形の面積の求め方 公式と計算例

台形の面積の求め方 公式と計算例

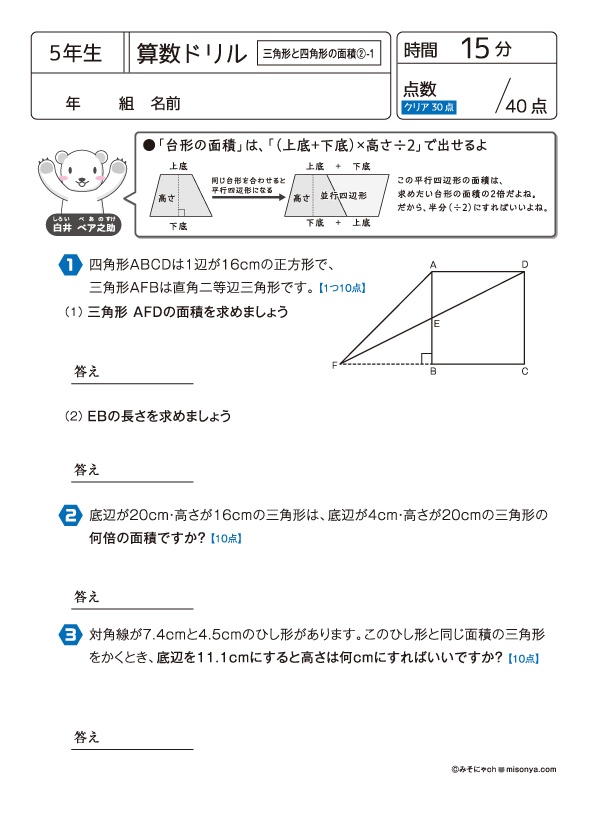
無料の学習プリント 小学5年生の算数ドリル 三角形と四角形の面積2 みそにゃch

3

なぜ底辺と高さが同じなら全ての三角形の面積は等しいのか 数学が嫌いなんです

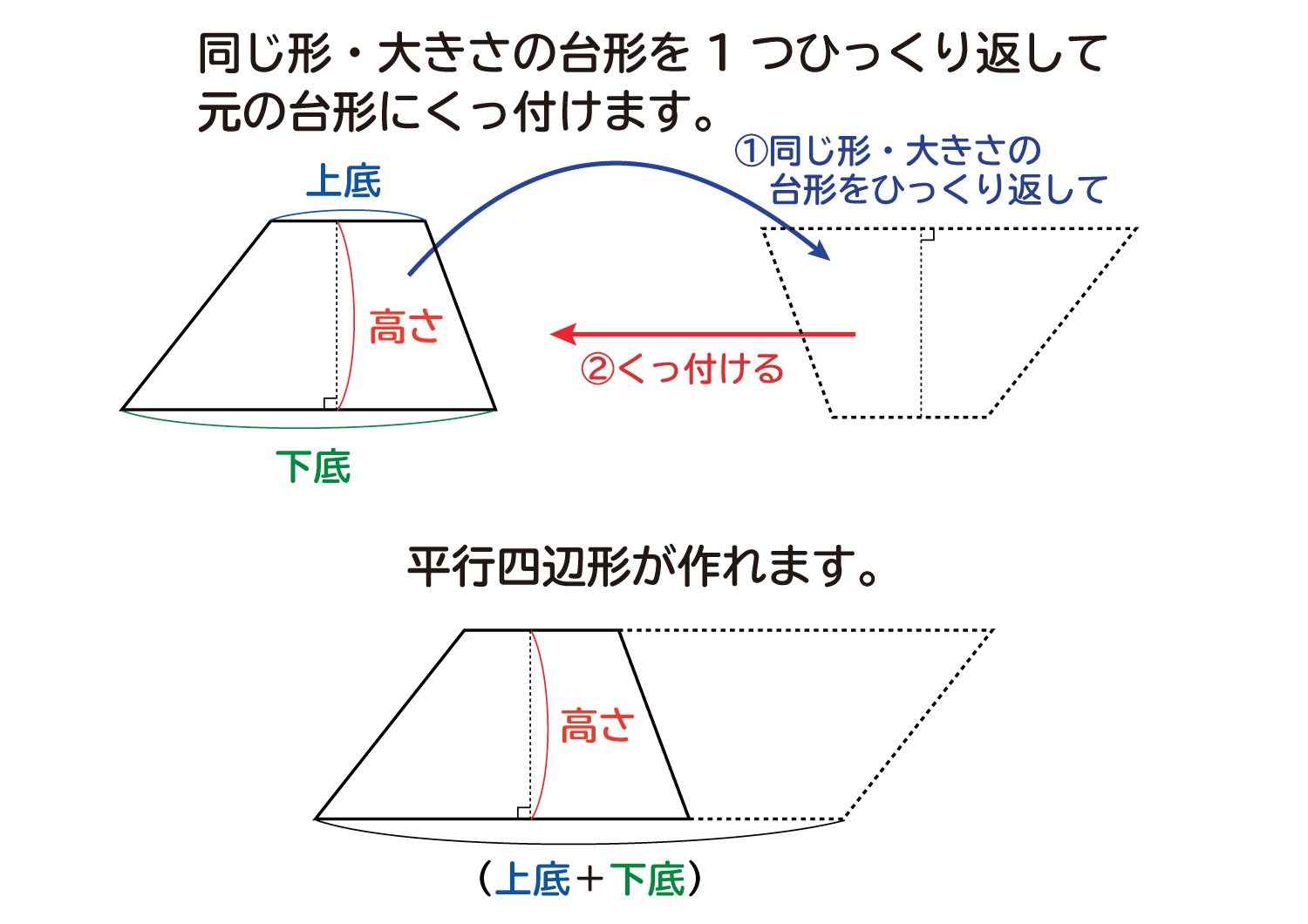
なぜ 台形の面積は 上底 下底 高さ 2 なのか を説明します おかわりドリル

三角形 四角形の面積 Ict教材eboard イーボード

台形の面積 数学が嫌いなんです

三角形と台形の面積

台形をニ等分する直線 女子学院中学 ２０１３年 パズル おもしろ算数問題

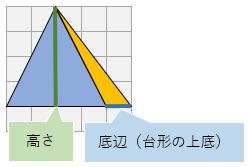
台形の面積の求め方 算数の公式は覚えるな Sundry Street

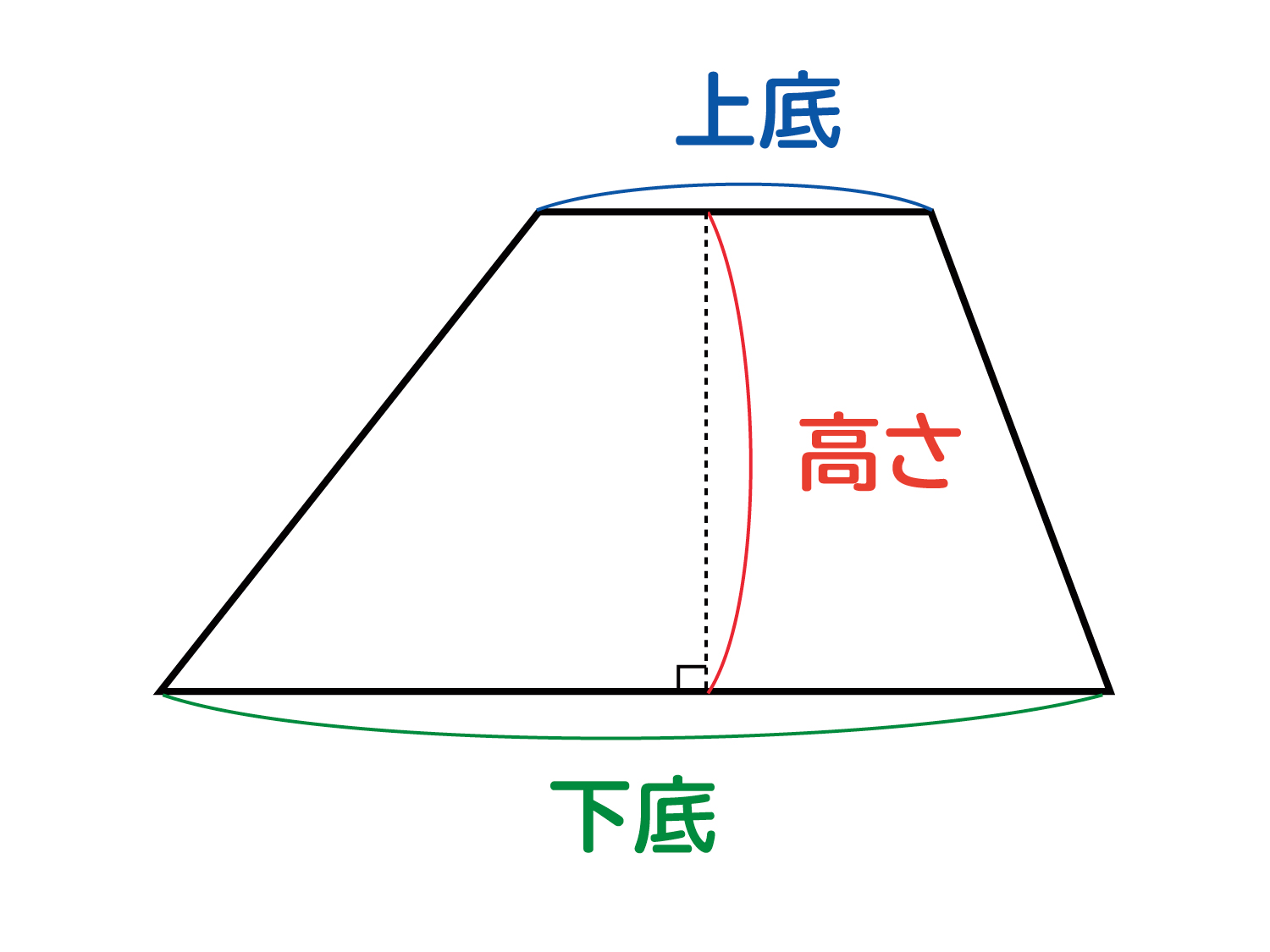
なぜ 台形の面積は 上底 下底 高さ 2 なのか を説明します おかわりドリル

台形の面積の求めかたは 忘れても大丈夫 公式は自分でつくろう

算数 図形

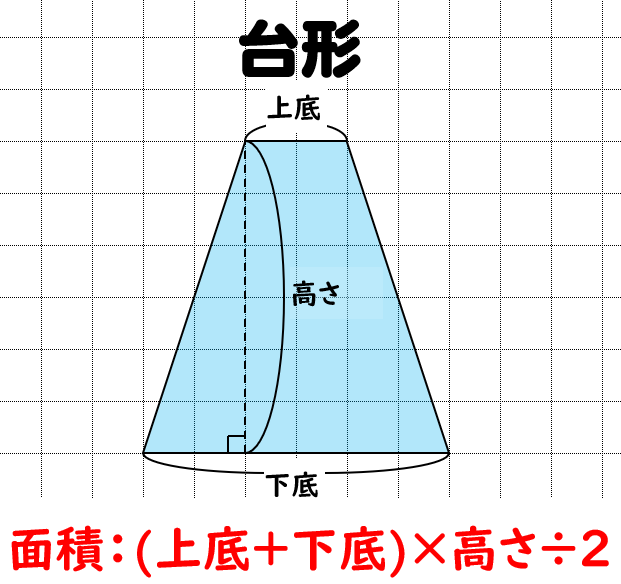
台形の面積の公式 小学生に教えるための分かりやすい解説 数学fun

台形の面積公式 算数と図形 理数系学習サイト Kori

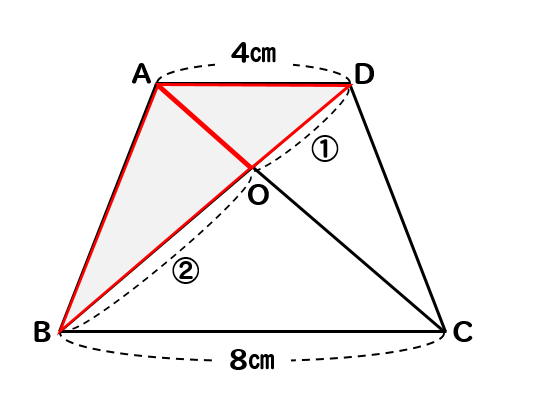
相似 台形と面積比の問題を徹底解説 数スタ

５年算数 台形の面積 指導実践 ネコ好きな学校の先生の日常

いま一度確認 台形の面積の求め方は 図のハイライトされた部分の面積は 毎日脳トレ クイズ Dアプリ レビュー

台形とは 定義や 台形の面積の公式をわかりやすく解説 受験辞典

台形の底辺は 1分でわかる意味 計算 求め方 上辺 面積との関係

算数 テーマ別 ポイント集 平面図形 10 14 中学受験の勉強法 偏差値アップの学習法

1

簡単に面積が何倍か求められる 使える編 苦手な数学を簡単に

2

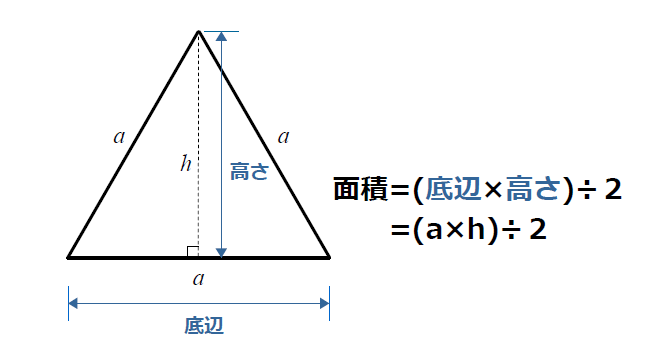
正三角形の面積計算 ゆるゆるプログラミング

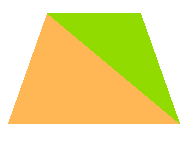
台形 通信用語の基礎知識

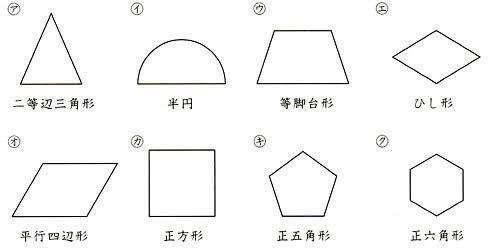
高校受験対策laf先生 意外と忘れている算数 面積の公式編 正方形 一辺 一辺 長方形 縦 横 平行四辺形 底辺 高さ 三角形 底辺 高さ 2 台形 上底 下底 高さ 2 ひし形 対角線 対角線 2 円 半径 半径

盲点の英単語 その8 1 三角形 台形の面積を求める 中学の英語をあなどってはいけない

算数 本当に 分かる という事 公式の意味を考えよう エース学院

台形の 面積 底辺 角度 から 上辺と高さ の求め方 台形の面積 数学 教えて Goo

台形の底辺は 1分でわかる意味 計算 求め方 上辺 面積との関係

５年算数三角形と四角形の面積2 教え方 台形 ひし形

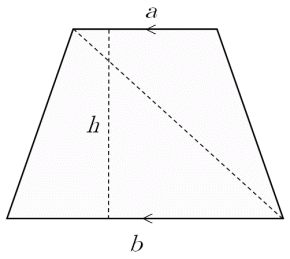
初等幾何 台形の面積はなぜ 上底 下底 高さ ２ なのか 大人が学び直す数学

算数 テーマ別 ポイント集 平面図形 10 14 中学受験の勉強法 偏差値アップの学習法

台形abcdと Cobの面積の比を求めよ という問題です Clearnote

小学5年生 ひし形 台形の面積 算数 Active Learning 学院

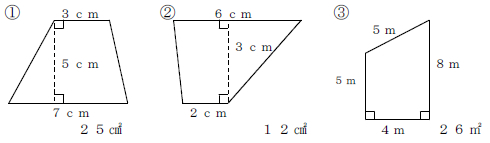
第５学年 面積 台形 私の実践 私の工夫アーカイブ一覧 授業支援 サポート資料 算数 小学校 知が啓く 教科書の啓林館

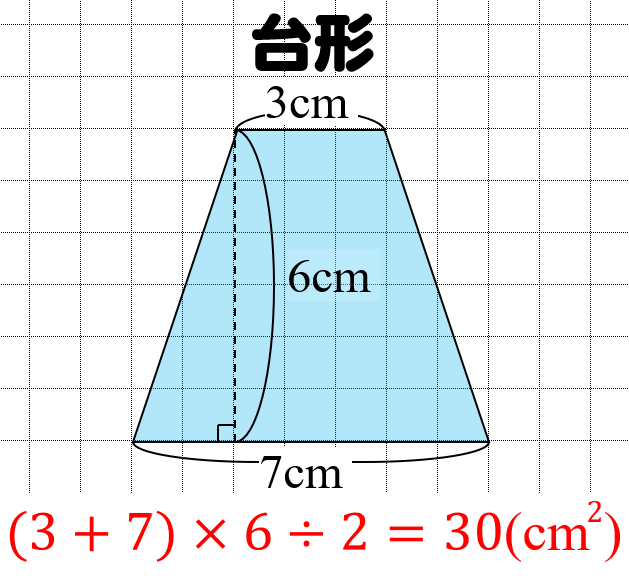
台形の面積の公式 小学生に教えるための分かりやすい解説 数学fun

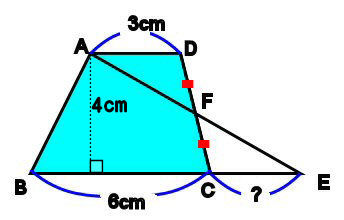
台形と三角形

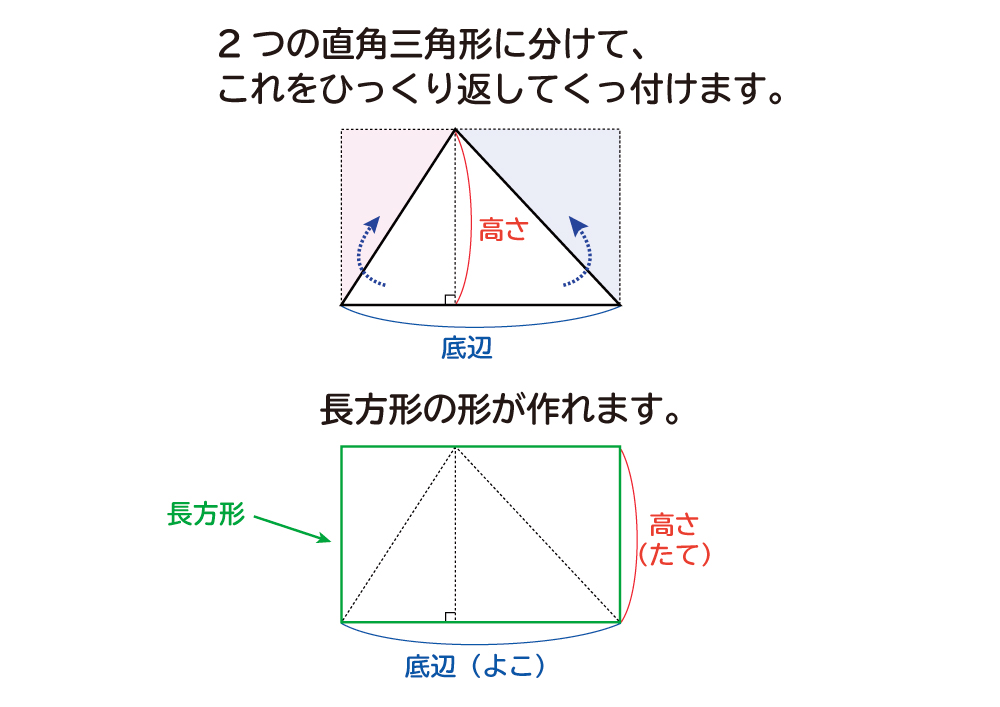
なぜ 三角形の面積は 底辺 高さ 2 なのか を説明します おかわりドリル

台形の面積の求めかたは 忘れても大丈夫 公式は自分でつくろう

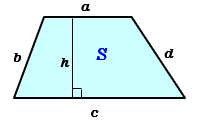
台形の１辺 面積 ３辺の長さと高さから 高精度計算サイト

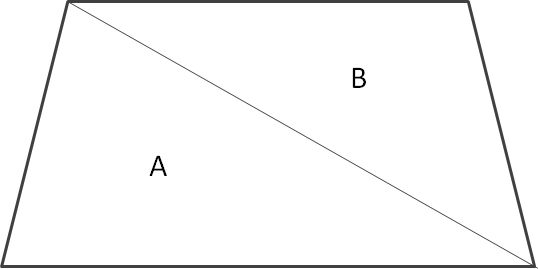
台形の面積の計算機 二等分 求め方 Nujonoa Blog

Kyoiku Shuppan Co Jp

小学生の算数が基礎から子どもは学べ 大人は教えられる算数サイト